J Value Torsion

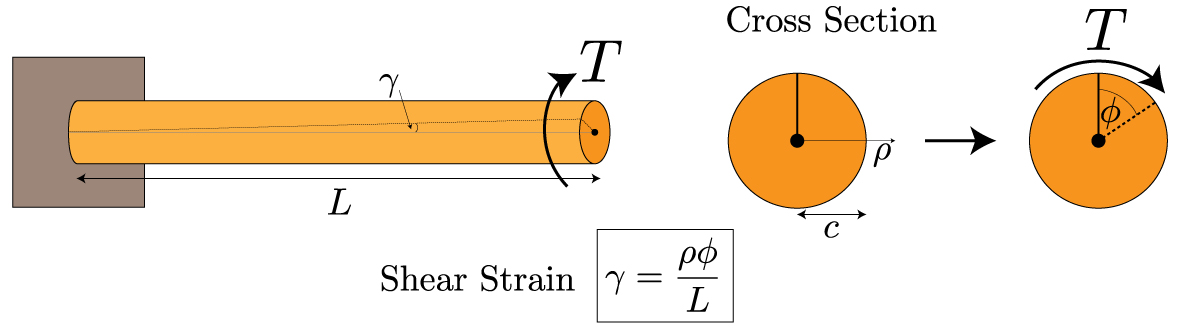
J Polar Moment of Inertia of Area m4 ft4 Note. Conversely shear strain is at its maximum value γ γ max at the outer surface of the shaft r r max.

Mechanics Of Materials Torsion Mechanics Of Slender Structures Boston University

T torque or twisting moment Nm lbin J polar moment of inertia or polar second moment of area about shaft axis m 4 in 4 τ shear stress at outer fibre Pa psi r radius of the shaft m in.

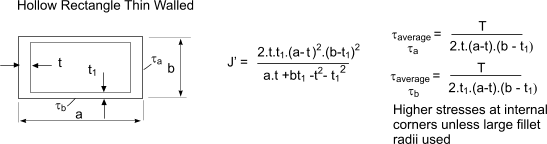
J value torsion. Area moment of inertia polar moment of areainertia or second area moment in the case of a. The Polar Moment of Inertia of an Area is a measure of a shafts ability to resist torsion. 852 Torsion of Non-circular and Thin-walled Sections 143 In the absence of Table 51 however it is possible to reduce the above equations to the following approximate forms.

τr TJ In above equation τ is the torsional stresses produce in the shaft r is the radius of the shaft T is the torque applied at the end of the shaft and J is the second polar moment of inertia of the shaft. J is the polar moment of inertia for the cross-section units. T J T r τ J T ℓ G φ displaystyle T frac J_ text T rtau frac J_ text T ell Gvarphi where.

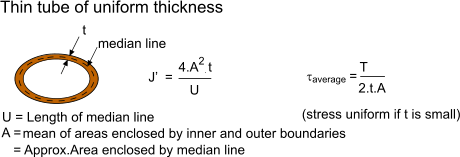
The corrective term for warping inertia is usually discarded. J r2 dA is the polar moment of intertia of the cross sectional area. The mean radius is Rm.

Torsion modes are discussed starting from equation 241 where the area polar moment of inertia J is replaced by the torsion constant J T to account for the warping of the cross-sections. Specialize the general equations of stress equilibrium. J u bd 4 - 6b 2 d 2 12 bd 10410 6From Table It is necessary to locate the point subject to the highest shear stressFor a weld subject to only torsion this would be simply at the point furthest from the COG.

For a tubular shaft J p2R 4 - r 4 where r is the inner radius. The value k can be approximated using the following formula. The Torsion constant J for Hollow Rolled Sections are calculated as follows.

I is the second moment of area t is the thickness of section h is the mean perimeter 2 B - t D - t - 2 R c 4 -. It is used in calculating the buckling moment resistance of laterally unsupported beams and torsional-flexural buckling of compression members in accordance with. M 4 or mm 4 Notice that the higher the radius r the higher the torsional shear stress.

K 1063 t b 0052 t b2 k 1 063 t b 0052. Since first working on the PD motors we found the setting of the torsion value a bit of a mystery. Its units are mm 4 or inches 4.

This is sometimes referred to as the second moment of inertia but since that already has a well-established meaning regarding the dynamic motion of objects lets not confuse things here. If the shaft has a length L 100 mm and has a shear modulus G 200 GPa then the twist f TLJG 4 x 10-3 radians 003 degrees a suitable design value. Now for a solid circular shaft we have J πc42 Further for any point at distance r from the center of the shaft we have the shear stress τ.

Like for the torsion problem. All torsion problems that you are expected to answer can be solved using the following formula. The torsional rigidity with SI units Nm 2 rad And the torsional stiffness.

Ijj 0 no body forces to the torsion problem no need to express them in terms of the strains or displacement assumptions as we will use a stress function Solution. J 13 t 3 h 2k A h where. Break the section down into a series of rectangles with sides b b and t t with t b t b.

3Tee section 305x457x127 calculated J 296 cm 4. Second polar moment of inertia of the shaft can be finding out by following formula where D is diameter of the shaft. J is the torsional constant.

The only non-trivial equation is the third. However because the weld is subject to torsion and. The Polar Moment of Inertia is defined with respect to an axis perpendicular to the area considered.

The torsion value is located in VCDSEngine Module block 4 torsion value. Calculate the Torsion Constant J of a beam section Moment of Inertia For instance if youre looking how to calculate the moment of inertia of a rectangle you can use the tool above simply by selecting rectangle from the drop down list then entering some dimensions for height and width eg. τ displaystyle tau tau is the maximum shear stress at the outer surface.

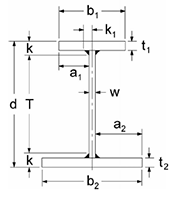
The beam will be subjected to stresses due to torsion as well as due to bending. Cw warping constant If the loads are applied away from the shear centre axis torsion besides flexure will be the evident result. 3 shows a thin-walled cylindrical bar subjected to a twisting moment T.

J kbt3 3 J k b t 3 3. Similar calculations can be used for a propeller shaft where the torque is that required to turn the propeller. Table value 297 η 110.

With SI units Nmrad. BEAMS SUBJECTED TO BENDING AND TORSION-I where O shear centre. However early on we had a Passat Wagon that lost 4 mpg when we set the torsion value to 00.

JT is the torsion constant for the section. We tended to figure that 00 was a good figure and originally let it go at that. Table value 312 η 106 4Tee section 133x102x137 calculated J 269 cm 4.

In the notes and tables below J is used throughout for the torsion constant for circular and non circular sections. Hi Mahdi J is the torsion constant this is related to the second moment of area. It owes much to the earlier SCI publication P057 Design of members subject to combined bending and torsion prepared by Nethercot Salter and Malik and published in 1989.

Although the scope is similar and the fundamental theory is unchanged. Thus the maximum shear stress τmax TcJ The above equation is called the torsion formula. Torsional Rigidity GJ and Stiffness GJL Inverting the previous relation we can define two quantities.

T T rmax 3 183 -3d db3 18bI 53 and 42TW 42TW GA4 Gd4b4 j- - - 54 where A is the cross-sectional area of the section bd and J bd12b2 d2. The bending resistance formula in which the torsional constant is used is. T is the applied torque or moment of torsion in Nm.

Simplified method for open sections. In this equation J denotes the second polar moment of area of the cross section. For circular hollow sections.

J torsion constant. I also known as. 311 322 0 68.

J TR J Tr τ. φ max The polar second moment of area J π 2 Ro 2 R i 2 For thin walled tubes with t. Similar to the modulus of elasticity E for a body under tension a shaft in torsion has a property known as the shear modulus also referred to as the modulus of elasticity in shear or the modulus of rigidity.

Venant torsional constant J measures the resistance of a structural member to pure or uniform torsion. This publication provides guidance on the design of steel beams subject to torsion. In structural steel design the Torsion Constant J represents the ability of the steel beam to resist torsion ie.

J 2I For square and rectangular hollow sections.

Torsion Equations Roy Mech

Torsion Equations Roy Mech

What Is The Torsion Constant